Calculus Applied!
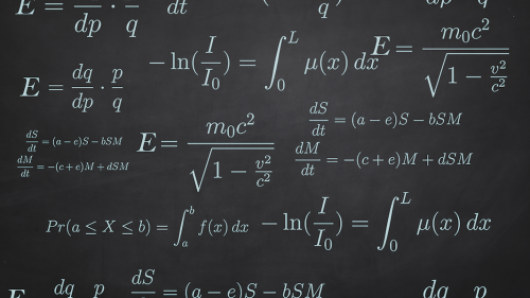
- Intermediate
Add a Verified Certificate for $209
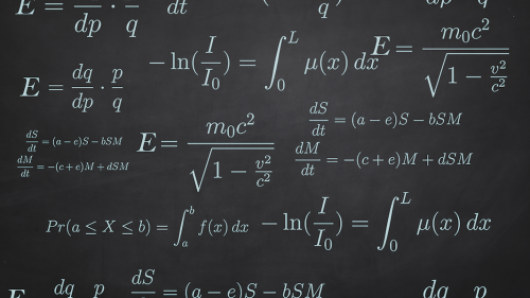
Authentic examples and case studies of how calculus is applied to problems in other fields
How to analyze mathematical models, including variables, constants, and parameters
Appreciation for the assumptions and complications that go into modeling real world situations with mathematics
How standardized test makers use functions to analyze the difficulty of test questions
How economists model interaction of price and demand using rates of change, in a historical case of subway ridership
How an x-ray is different from a CT-scan, and what this has to do with integrals
In this course, we go beyond the calculus textbook, working with practitioners in social, life, and physical sciences to understand how calculus and mathematical models play a role in their work.
Through a series of case studies, you’ll learn about a wide range of applications, from predator-prey models to how statisticians use functions to model data.
With real practitioners as your guide, you’ll get hands-on experience with data and graphs, equations, calculus computations, and educated guesses and predictions.
This course provides a unique supplement to a course in single-variable calculus. Key topics include the application of derivatives, integrals and differential equations, mathematical models and parameters.
This course is for anyone who has completed or is currently taking a single-variable calculus course (differential and integral), at the high school (AP or IB) or college/university level. You will need to be familiar with the basics of derivatives, integrals, and differential equations, as well as functions involving polynomials, exponentials, and logarithms.
This is a course to learn applications of calculus to other fields, and NOT a course to learn the basics of calculus. Whether you’re a student who has just finished an introductory calculus course or a teacher looking for more authentic examples for your classroom, there is something for you, and we hope you’ll join us!